25 GnuPG und das Geheimnis der großen Zahlen

Inhalt

25 GnuPG und das Geheimnis der großen Zahlen

Kryptografie für Nicht-Mathematiker
Es ist schon versucht worden, den RSA-Algorithmus, auf dem GnuPG basiert⁵, zu „knacken“, also einen privaten Schlüssel zu berechnen, wenn man lediglich den öffentlichen Schlüssel kennt. Diese Berechnung ist aber noch nie für Schlüssellängen von 1.024 Bit und mehr gelungen, wie sie in GnuPG verwendet werden. Es ist zwar theoretisch möglich, aber praktisch nicht durchführbar. Denn selbst bei vielen Jahren Rechenzeit und Abertausenden von vernetzten Rechnern würde nicht genügend Speicher zur Verfügung stehen, um den letzten Schritt dieser Berechnung durchführen zu können.

Es kann allerdings durchaus möglich sein, dass eines Tages eine geniale Idee die Mathematik revolutioniert und eine schnelle Lösung des mathematischen Problems liefert, welches hinter RSA steckt - allerdings wohl nicht sehr bald.

Das Bundesamt für Sicherheit in der Informationstechnik (BSI) veröffentlicht von Zeit zu Zeit Prognosen und Einschätzungen, welche Schlüssellängen noch wie viele Jahre für absolute Geheimhaltung benutzt werden sollen. GnuPG erfüllt mit seinen Standardeinstellungen diese Mindestanforderungen. Wie im vorigen Kapitel schon angerissen, ist die Mathematik der mit Abstand sicherste Teil der praktisch angewandten Kryptografie.

Im Folgenden erfahren Sie, wie diese mathematische Methode funktioniert. Nicht in allen Einzelheiten (das würde den Rahmen dieser Anleitung bei Weitem sprengen), aber doch so, dass Sie bei etwas Mitrechnen selbst mathematisch korrekt ver- und entschlüsseln können und dabei das „Geheimnis der großen Zahlen“ entdecken.

Man kann diese komplexe mathematische Methode auch als Nichtmathematiker verstehen, da nur die Grundrechenarten benötigt werden. Wie gesagt: Hier beginnt der Kürteil, und bei der Kür geht es immer etwas mehr zur Sache als im Pflichtprogramm. Letztendlich versteht man dann aber, warum GnuPG sicher ist.

Zwei Begriffsklärungen vorneweg:

Die Verschlüsselung mit GnuPG basiert auf dem sogenannten RSA-Algorithmus⁶. RSA steht für die Nachnamen von Ron Rivest, Ami Shamir und Ben Adleman, die diesen Algorithmus im Jahr 1978 entdeckt haben. Dieser Algorithmus verwendet einen Typ der Arithmetik, die Rechnen mit Restklassen oder „Modulo-Arithmetik“ heißt.

25.1 Das Rechnen mit Restklassen

Wenn man mit Restklassen rechnet, so bedeutet dies, dass man nur mit dem „Rest“ rechnet, der nach einer ganzzahligen Teilung durch eine bestimmte Zahl übrigbleibt. Diese Zahl, durch die geteilt wird, nennt man den „Modul“ oder die „Modulzahl“. Wenn Sie beispielsweise mit dem Teiler oder der Modulzahl 5 rechnen, sagt man auch, „ich rechne modulo 5“.

Wie das Rechnen mit Restklassen - auch Modulo-Arithmetik oder Kongruenzrechnung genannt - funktioniert, kann man sich gut klarmachen, wenn man sich das Zifferblattes einer Uhr vorstellt:

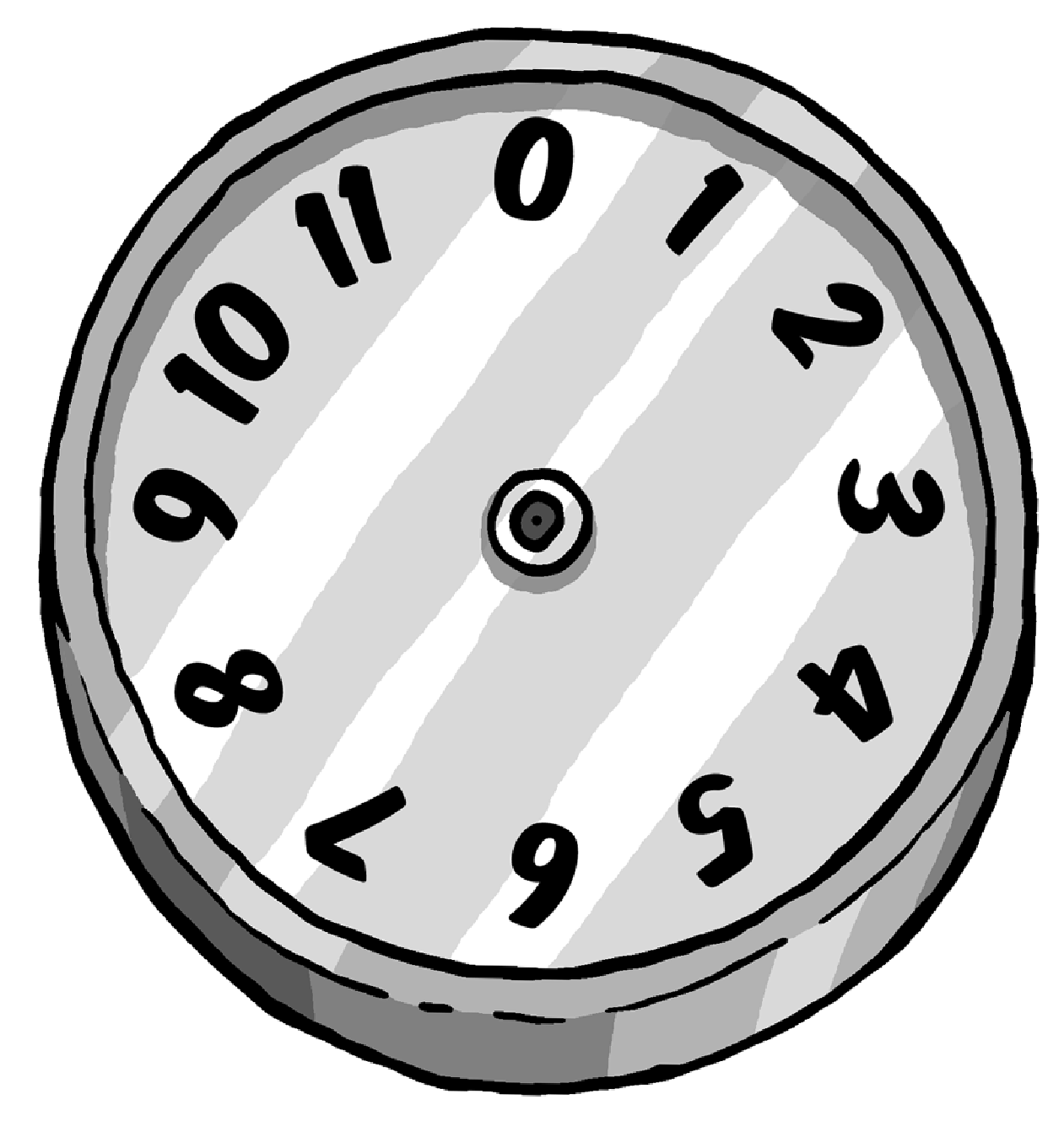
Diese Uhr ist ein Beispiel für das Rechnen mit modulo 12 (die Modulzahl ist also 12) - eine Uhr mit einem normalen Zifferblatt, allerdings mit einer 0 anstelle der 12. Sie können damit Modulo-Arithmetik betreiben, indem Sie einfach den gedachten Zeiger bewegen.

Um beispielsweise 3 + 2 zu rechnen, beginnen Sie bei der Ziffer 2 und drehen den Zeiger um 3 Striche weiter (oder Sie starten bei der 3 und drehen 2 Striche weiter, was natürlich auf dasselbe hinausläuft). Das Ergebnis ist 5.

Zählt man auf diese Weise 7 + 8 zusammen, erhält man 3. Denn 3 ist der Rest, wenn man 15 (also 7 + 8) durch 12 teilt. Um 5 mit 7 zu multiplizieren, beginnt man bei 0 und dreht 7 mal jeweils um 5 Striche weiter (oder auch bei 0 beginnend 5 mal um 7 Striche). In beiden Fällen bleibt der Zeiger bei 11 stehen. Denn 11 ist der Rest, wenn 35 (also 7 * 5) durch 12 geteilt wird.

Beim Rechnen mit Restklassen addieren und teilen Sie Zahlen also nach den normalen Regeln der Alltagsarithmetik, verwenden dabei jedoch immer nur den Rest nach der Teilung. Um anzuzeigen, dass Sie nach den Regeln der Modulo-Arithmetik und nicht nach denen der üblichen Arithmetik rechnen, schreibt man den Modul (Sie wissen schon - den Teiler) dazu. Man sagt dann z.B. „4 modulo 5“, schreibt aber kurz „4 mod5“.

Bei Modulo-5 z.B. hat man dann eine Uhr, auf deren Zifferblatt es nur die 0, 1, 2, 3 und 4 gibt. Also:

4 mod5 + 3 mod5 = 7 mod5 = 2 mod5

Anders ausgedrückt, ist in der Modulo-5-Arithmetik das Ergebnis aus 4 plus 3 gleich 2.
Ein weiteres Beispiel in Modulo-5-Arithmetik:

8 mod5 + 6 mod5 = 14 mod5 = 4 mod5

Sie sehen auch, dass es egal ist, in welcher Reihenfolge Sie vorgehen, weil Sie nämlich auch schreiben können:

8 mod5 + 6 mod5 = 3 mod5 + 1 mod5 = 4 mod5

Denn 3 ist dasselbe wie 8, und 1 dasselbe wie 6, da Sie sich ja nur für den jeweiligen Rest nach der Teilung durch 5 interessieren.

An den letzten Beispielen wird deutlich, dass bei der Modulo-Arithmetik jederzeit ein ganzzahliges Vielfaches der Modulzahl (hier 5) addiert werden kann, das Rechenergebnis aber stets dasselbe bleibt.

Dieses Schema funktioniert auch beim Multiplizieren.

Ein Beispiel:

4 mod5 * 2 mod5 = 8 mod5 = 3 mod5

Ebenso können Sie schreiben:

9 mod5 * 7 mod5 = 63 mod5 = 3 mod5

da Sie einfach 60, also 5 * 12, abziehen können.

Man könnte aber auch schreiben:

9 mod5 * 7 mod5 = 4 mod5 * 2 mod5 = 8 mod5 = 3 mod5

denn 4 entspricht 9, und 2 entspricht 7, wenn Sie nur den Rest nach Teilung durch 5 betrachten.

Wiederum können Sie feststellen, dass es egal ist, wenn Sie das Vielfache von 5 einfach weglassen.

Da dadurch alles einfacher wird, machen Sie das, bevor Sie Zahlen addieren oder multiplizieren. Das bedeutet, dass Sie sich lediglich um die Zahlen 0, 1, 2, 3 und 4 kümmern müssen, wenn Sie mit der Modulo-5-Arithmetik rechnen. Denn Sie können ja alles, was durch 5 teilbar ist, weglassen.

Noch drei Beispiele mit anderen Modulzahlen:

1. [I.] 5 mod11 * 3 mod11 = 15 mod11 = 4 mod11
2. [II.] 2 mod7 * 4 mod7 = 1 mod7
3. [III.] 13 mod17 * 11 mod17 = 7 mod17
   Das letzte Beispiel wird klar, wenn man bedenkt, dass in normaler Arithmetik gerechnet 13 * 11 = 143 und 143 = 8 * 17 + 7 ist.

25.2 RSA-Algorithmus und Rechnen mit Restklassen

Computer speichern Buchstaben als Zahlen. Alle Buchstaben und Symbole auf der Computertastatur werden in Wirklichkeit als Zahlen gespeichert, die typisch zwischen 0 und 255 liegen.

Sie können also eine Nachricht auch in eine Zahlenfolge umwandeln. Nach welcher Methode (oder welchem Algorithmus) dies geschieht, wird im nächsten Abschnitt beschrieben. Darin wird die Methode vorgestellt, nach der die Verschlüsselung mit GnuPG funktioniert: den RSA-Algorithmus. Dieser Algorithmus wandelt eine Zahlenfolge (die ja eine Nachricht darstellen kann) so in eine andere Zahlenfolge um (also eine Transformation), dass die Nachricht dabei verschlüsselt wird. Wenn man dabei nach dem richtigen Verfahren vorgeht, wird die Nachricht sicher kodiert und kann nur noch vom rechtmäßigen Empfänger dekodiert werden.

Das sind die Grundlagen des RSA-Algorithmus:

Sie selbst haben bei der Erzeugung eines Zertifikats während der Eingabe Ihrer Passphrase zwei große Primzahlen erzeugt, ohne es zu bemerken (dieser werden mit p und q bezeichnet). Nur Sie -­ oder in der Praxis Ihr Rechner -­ kennen diese beiden Primzahlen und Sie müssen für deren Geheimhaltung sorgen.

Es werden daraus nun drei weitere Zahlen erzeugt:

Die erste Zahl

ist das Ergebnis der Multiplikation der beiden Primzahlen, also ihr Produkt. Dieses Produkt wird als Modulus und mit dem Buchstaben n bezeichnet. Dies ist die Modulzahl, mit der Sie später immer rechnen werden.

Die zweite Zahl

ist der sogenannte öffentliche Exponent e und eine Zahl, an die bestimmte Anforderungen gestellt werden: teilerfremd zu (p-1)(q-1). Häufig wird hier 41 oder 65537 benutzt.

Die dritte Zahl

wird errechnet aus dem öffentlichen Exponent (der zweiten Zahl) und den beiden Primzahlen. Diese Zahl ist der geheime Exponent und wird mit d bezeichnet. Die Formel zur Berechnung lautet:

d = e^-1 mod(p - 1)(q -1)

Die erste und die zweite Zahl werden veröffentlicht ­- das ist Ihr öffentlicher Schlüssel. Beide werden dazu benutzt, Nachrichten zu verschlüsseln. Die dritte Zahl muss von Ihnen geheim gehalten werden ­- es ist Ihr geheimer Schlüssel. Die beiden Primzahlen (p und q) werden danach nicht mehr benötigt.

Wenn eine verschlüsselte Nachricht empfangen wird, kann sie entschlüsselt werden mit Hilfe der ersten (n) und der dritten Zahl (d). Nur der Empfänger kennt beide Schlüsselteile ­- seinen öffentlichen und seinen geheimen Schlüssel. Der Rest der Welt kennt nur den öffentlichen Schlüssel (n und e).

Die Trick des RSA-Algorithmus liegt nun darin, dass es unmöglich ist, aus dem öffentlichen Schlüsselteil (n und e) den geheimen Schlüsselteil (d) zu errechnen und damit die Botschaft zu entschlüsseln - denn: Nur wer im Besitz von d ist, kann die Botschaft entschlüsseln.

25.3 RSA-Verschlüsselung mit kleinen Zahlen

Sie verwenden hier erst einmal kleine Zahlen, um deutlich zu machen, wie die Methode funktioniert. In der Praxis verwendet man jedoch viel größere Primzahlen, die aus vielen Ziffern bestehen.

Nehmen Sie die Primzahlen 7 und 11. Damit verschlüsseln Sie Zahlen ­- oder Buchstaben, was für den Rechner dasselbe ist - nach dem RSA-Algorithmus.

Und zwar erzeugen Sie zunächst den öffentlichen Schlüssel.

Die erste Zahl

ist 77, nämlich das Ergebnis der Multiplikation der beiden Primzahlen, 7 und 11. 77 dient Ihnen im weiteren Verlauf als Modulus zur Ver- und Entschlüsselung.

Die zweite Zahl

ist der öffentliche Exponent. Sie wählen hier 13.

Die dritte Zahl

ist der geheime Schlüssel. Diese Zahl wird wie folgt errechnet:

Zunächst ziehen Sie von Ihren Primzahlen 7 und 11 jeweils die Zahl 1 ab (also 7 - 1 und 11 - 1) und multiplizieren die beiden resultierenden Zahlen miteinander. In dem Beispiel ergibt das 60: ( 7 - 1 ) * ( 11 - 1) = 60. 60 ist Ihre Modulzahl für die weiterführende Berechnung des geheimen Schlüssels (sie ist aber nicht mit dem eigentlichen Modulus 77 zu verwechseln).

Sie suchen jetzt eine Zahl, die multipliziert mit dem öffentlichen Schlüssel die Zahl 1 ergibt, wenn man mit dem Modul 60 rechnet:

13 mod60 * ? mod60 = 1 mod60

Die einzige Zahl, die diese Bedingung erfüllt, ist 37, denn

13 mod60 * 37 mod60 = 481 mod60 = 1 mod60

37 ist die einzige Zahl, die multipliziert mit 13 die Zahl 1 ergibt, wenn man mit dem Modul 60 rechnet.

Sie verschlüsseln mit dem öffentlichen Schlüssel eine Nachricht

Nun zerlegen Sie die Nachricht in eine Folge von Zahlen zwischen 0 und 76, also 77 Zahlen, denn sowohl Verschlüsselung als auch Entschlüsselung verwenden den Modul 77 (das Produkt aus den Primzahlen 7 und 11).

Jede einzelne dieser Zahlen wird nun nach der Modulo-77-Arithmetik 13 mal mit sich selbst multipliziert. Sie erinnern sich: Die 13 ist Ihr öffentlicher Schlüssel.

Nehmen Sie ein Beispiel mit der Zahl 2: Sie wird in die Zahl 30 umgewandelt, weil 2 * 2 * 2 * 2 * 2 * 2 * 2 * 2 * 2 * 2 * 2 * 2 * 2 * 2 = 2¹³ = 8192 = 30 mod77 sind.

Ein weiteres Beispiel: 75 wird in die Zahl 47 umgewandelt, denn 75 wird 13 mal mit sich selbst multipliziert und durch 77 geteilt, so dass der Rest 47 entsteht.

Wenn man eine solche Rechnung für alle Zahlen zwischen 0 und 76 durchführt und die Ergebnisse in eine Tabelle einsetzt, sieht diese so aus:

Tabelle 1


In der linken Spalte stehen die 10er-Stellen, in der oberen Zeile die 1er-Stellen.

Entschlüsseln Sie eine Nachricht mit dem privaten Schlüssel

Um das Beispiel mit der 2 von oben umzukehren, also die Nachricht zu dekodieren, multiplizieren Sie 30 (die umgewandelte 2) 37 mal mit sich selbst (30³⁷). Das Ergebnis wird modulo der Modulzahl 77 gerechnet. Sie erinnern sich: 37 ist der geheime Schlüssel.

Diese wiederholte Multiplikation ergibt eine Zahl, die 2 mod77 ist.

Das andere Beispiel: Die Zahl 47 mod77 wird zur Zahl 75 mod77 dekodiert.

Tabelle 2 zeigt die genaue Zuordnung der 77 Zahlen zwischen 0 und 76.

Tabelle 2: Zahlentransformation modulo 77, unter Verwendung des geheimen Schlüssels 37


Um eine Zahl mit Tabelle 2 zu transformieren, gehen Sie nach der gleichen Methode vor wie bei Tabelle 1. Ein Beispiel: 60 wird transformiert in die Zahl in Zeile 60 und Spalte 0. Also wird 60 zu 25 transformiert.

Das überrascht nicht, denn wenn man davon ausgeht, dass Sie bei der Umwandlung von 25 mit Hilfe von Tabelle 1 als Ergebnis 60 erhalten, dann sollten Sie auch bei der Transformation von 60 mit Hilfe von Tabelle 2 zum Ergebnis 25 gelangen. Dabei haben Sie den öffentlichen Schlüssel, hier die 13, zur Umwandlung bzw. Kodierung einer Zahl verwendet und den geheimen Schlüssel 37, um sie zurückzuwandeln bzw. zu dekodieren. Sowohl für die Verschlüsselung als auch für die Entschlüsselung haben Sie sich der Modulo-77-Arithmetik bedient.

Zusammenfassung

Sie haben ...

• durch den Rechner zwei zufällige Primzahlen erzeugen lassen;
• daraus das Produkt und den öffentlichen und den geheimen Schlüssel gebildet;
• mit dem öffentlichen Schlüssel eine Nachricht verschlüsselt;
• mit dem geheimen Schlüssel eine Nachricht entschlüsselt.

Diese beiden Primzahlen können so groß gewählt werden, dass es unmöglich ist, sie einzig aus dem öffentlich bekannt gemachten Produkt zu ermitteln. Das begründet die Sicherheit des RSA-Algorithmus.

Sie haben gesehen, dass die Rechnerei sogar in diesem einfachen Beispiel recht aufwändig geworden ist. In diesem Fall hat die Person, die den Schlüssel öffentlich gemacht hat, die Zahlen 77 und 13 als öffentlichen Schlüssel bekanntgegeben. Damit kann jedermann dieser Person mit der oben beschriebenen Methode -­ wie im Beispiel der Tabelle 1 -­ eine verschlüsselte Zahl oder Zahlenfolge schicken. Der rechtmäßige Empfänger der verschlüsselten Zahlenfolge kann diese dann mit Hilfe der Zahl 77 und dem geheimen Schlüssel 37 dekodieren.

In diesem einfachen Beispiel ist die Verschlüsselung natürlich nicht sonderlich sicher. Es ist klar, dass 77 das Produkt aus 7 und 11 ist.

Folglich kann man den Code in diesem einfachen Beispiel leicht knacken. Ein aufmerksamer Leser wird auch bemerkt haben, dass etliche Zahlen, z.B. die Zahl 11 und ihr Vielfaches (also 22, 33 etc.) und die benachbarten Zahlen sich in sich selbst umwandeln.

Tabelle 3


Das erscheint als ein weiterer Schwachpunkt dieser Verschlüsselungsmethode: Man könnte annehmen, dass die Sicherheit des Algorithmus dadurch beeinträchtigt würde. Doch stellen Sie sich nun vor, das Produkt zweier großer Primzahlen, die auf absolut willkürliche Art und Weise gewählt werden, ergäbe:

114,381,625,757,888,867,669,235,779,976,146,612,010,
218,296,721,242,362,562,561,842,935,706,935,245,733,
897,830,597,123,563,958,705,058,989,075,147,599,290,
026,879,543,541

Hier ist überhaupt nicht mehr ersichtlich, welche die beiden zugrunde liegenden Primzahlen sind. Folglich ist es extrem aufwändig, aufgrund des öffentlichen Schlüssels den geheimen Schlüssel zu ermitteln. Selbst die schnellsten Rechnern der Welt würden sehr lange benötigen, die beiden Primzahlen zu errechnen.

Man muss die Primzahlen also nur groß genug wählen, damit ihre Berechnung aus dem Produkt so lange dauert, dass alle bekannten Methoden daran in der Praxis scheitern. Außerdem nimmt der Anteil der Zahlen, die in sich selbst transformiert werden -­ wie man sie oben in den Tabellen 1 und 2 findet - stetig ab, je größer die Primzahlen werden. Von Primzahlen in der Größenordnung, die Sie in der Praxis bei der Verschlüsselung verwenden, ist dieser Teil ist so klein, dass der RSA-Algorithmus davon in keiner Weise beeinträchtigt wird.

Je größer die Primzahlen, desto sicherer die Verschlüsselung. Trotzdem kann ein normaler PC ohne weiteres das Produkt aus zwei großen Primzahlen bilden. Kein Rechner der Welt dagegen kann aus diesem Produkt wieder die ursprünglichen Primzahlen herausrechnen -­ jedenfalls nicht in vertretbarer Zeit.

25.4 Die Darstellung mit verschiedenen Basiszahlen

Um zu verstehen, wie Nachrichten verschlüsselt werden, sollte man wissen, wie ein Rechner Zahlen speichert, und vor allem, wie sie in unterschiedlichen Zahlenbasen dargestellt werden können.

Dazu machen Sie sich zunächst mit den Zahlenpotenzen vertraut.

Zwei hoch eins, dargestellt als 2¹ = 2;
zwei hoch drei, dargestellt als 2³ = 2 * 2 * 2 = 8;
zwei hoch zehn, dargestellt als 2¹⁰ = 2*2*2*2*2*2*2*2*2*2 = 1024.

Jede Zahl hoch 0 ist gleich 1, z.B. 2⁰ = 1 und 5⁰ = 1. Verallgemeinert bedeutet dies, dass eine potenzierte Zahl so oft mit sich selbst multipliziert wird, wie es die Hochzahl (Potenz) angibt.

Das Konzept einer Zahlenbasis veranschaulicht z.B. ein Kilometerzähler im Auto: Das rechte Rad zählt nach jedem Kilometer eine Stelle weiter und zwar nach der vertrauten Abfolge der Zahlen:
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 0, 1, 2, ...

Jedesmal, wenn das rechte Rad wieder 0 erreicht, zählt das Rad links davon eine Stelle hoch. Und jedesmal, wenn dieses zweite Rad die 0 erreicht, erhöht das Rad links davon um eins ... und so weiter.

Das rechte Rad zählt die einzelnen Kilometer. Wenn es eine 8 angezeigt, dann sind dies 8 Kilometer. Das Rad links davon zeigt jeweils die vollen zehn Kilometer an: Eine 5 bedeutet 50 Kilometer. Dann folgen die Hunderter: Steht dort 7, dann bedeutet dies 700 Kilometer.

Nach dem gleichen Prinzip stellen Sie ja auch Ihre normale Zahlen mit den Ziffern 0 bis 9 dar.

„578“, z.B., bedeutet 5 * 10² + 7 * 10¹ + 8 * 10⁰ = 500 + 70 + 8, und dies entspricht 578.

Hier haben Sie die „5“ stellvertretend für fünfhundert, „7“ für siebzig und „8“ für acht. In diesem Fall ist die Basis 10, eine für Sie vertraute Basis.

Also steht die rechte Ziffer für die Einer der betreffenden Zahl (d.h., sie wird mit 1 multipliziert), die Ziffer links davon steht für die Zehner (d.h., wird mit 10 multipliziert), die nächste Ziffer wiederum für die Hunderter (d.h., sie wird mit 100 multipliziert) und so weiter. Da man Zahlen normalerweise zur Basis 10 darstellt, machen Sie sich nicht die Mühe, die Basis extra anzugeben. Formal würde man dies bei der Zahl 55 mit der Schreibweise 55₁₀ anzeigen, wobei die tiefgestellte Zahl die Basis anzeigt.

Wenn Sie Zahlen nicht zur Basis 10 darstellen, so müssen Sie dies mit Hilfe einer solchen tiefgestellten Basiszahl anzeigen.

Angenommen, die Anzeige des Kilometerzählers hätte statt der Ziffern 0 bis 9 nur noch 0 bis 7. Das rechte Rädchen würde nach jedem Kilometer um eine Ziffer höher zählen, wobei die Zahlenfolge so aussehen würde:

0, 1, 2, 3, 4, 5, 6, 7, 0, 1, 2, ...

Ihr dreistelliger Tacho zur Basis 8 stellt z.B. folgende Zahl dar:

356

Die 6 auf dem rechten Rädchen zählt einzelne Kilometer, also 6*8⁰=6 Kilometer.
Die 5 auf dem Rädchen in der Mitte für 5 * 8¹, also 40 Kilometer.
Die 3 links steht für je 64 Kilometer pro Umdrehung, also hier 3 * 8² Kilometer.

So rechnet man also mit Zahlen zur Basis 8. Ein Beispiel: 72₈ bedeutet 7 * 8¹ + 2 * 8⁰ = 58.
Bei dieser Art der Darstellung steht die „2“ aus der 72 für 2, aber die „7“ steht für 7 * 8.

Größere Zahlen werden schrittweise genauso aufgebaut, sodass 453₈ eigentlich 4 * 64 + 5 * 8 + 3 bedeutet, was 299₁₀ ergibt.
Bei 453₈ steht die „3“ für 3, die „5“ für 5 * 8 und die „4“ für 4 * 64, wobei sich die „64“ wiederum aus 8 * 8 herleitet.

Im angeführten Beispiel werden die Ziffern, von rechts nach links gehend, mit aufsteigenden Potenzen von 8 multipliziert. Die rechte Ziffer wird mit 8⁰ (das ist 1) multipliziert, die links daneben mit 8¹ (das ist 8), die nächste links davon mit 8² (das ist 64) und so weiter.

Wenn man Zahlen zur Basis 10 darstellt, gibt es keine höhere Ziffer als 9 (also 10 minus 1). Sie verfügen also über keine Ziffer, die 10 oder eine größere Zahl darstellt. Um 10 darzustellen, brauchen Sie zwei Ziffern, mit denen Sie dann die „10“ schreiben können.
Sie haben also nur die Ziffern 0 bis 9.
So ähnlich ist es, wenn Sie mit der Basiszahl 8 rechnen: Dann haben Sie nur die Ziffern 0 bis 7 zur Verfügung. Wollen Sie zu dieser Basis eine höhere Zahl als sieben darstellen, müssen Sie wieder zwei Ziffern verwenden - z.B. 9₁₀ ist 11₈, 73₁₀ ist 111₈.

Rechner speichern Zahlen als eine Folge von Nullen und Einsen. Man nennt dies Binärsystem oder Rechnen mit der Basiszahl 2, weil Sie nur die Ziffern 0 und 1 verwenden. Stellen Sie sich vor, Sie würden die Kilometer mit einem Tachometer zählen, auf dessen Rädchen sich nur zwei Ziffern befinden: 0 und 1. Die Zahl 10101₂ z.B. bedeutet im Binärsystem:

1*2⁴+0*2³+1*2²+0*2¹+1*2⁰ = 1 * 16 + 0 * 8 + 1 * 4 + 0 * 2 + 1 = 21

In der Informatik verwendet man auch Gruppen von acht Binärziffern, genannt „Byte“. Ein Byte kann Werte zwischen 0 - dargestellt als Byte 00000000₂ - und 255 - dargestellt als Byte 11111111₂ - annehmen. Ein Byte stellt also Zahlen zur Basis 2⁸ = 256 dar.

Zwei weitere Beispiele:

10101010₂ = 170

00000101₂ = 5

Da ein Rechner die Buchstaben, Ziffern und Satzzeichen als Bytes speichert, schauen Sie sich an, welche Rolle dabei die Darstellung zur Basis 256 spielt.

Nehmen Sie die Silbe „un“. Das „u“ wird im Rechner als 117 gespeichert und das „n“ als 110.

Diese Zahlenwerte sind für Rechner standardisiert und werden ASCII-Code genannt.

Sie können also die Silbe „un“ darstellen durch die Zahl:

117 * 2^8*1 + 110 * 2^8*0 = 117 * 256 + 110 = 30062

Entsprechend würde man die Buchstabenfolge „und“ mit der Zahl

117 * 2^8*2 + 110 * 2^8*1 + 100 * 2^8*0 = 117 * 65536 + 110 * 256 + 100 = 7695972

darstellen, denn das „d“ wird durch 100 repräsentiert.

Sie haben hier also Zahlen und Symbole, die auf der Computertastatur als normale Zahlen zur Basis 10 stehen, intern durch Zahlen zur Basis 2⁸ = 256 repräsentiert.

Entsprechend können Sie aus jeder Nachricht eine große Zahl machen. Aus einer langen Nachricht wird also eine gewaltig große Zahl. Und diese sehr große Zahl wollen Sie nun nach dem RSA-Algorithmus verschlüsseln.

Sie dürfen allerdings dabei die Zahl, zu der die Nachricht verschlüsselt wird, nicht größer werden lassen als das Produkt der Primzahlen (Modulus). Ansonsten bekommen Sie Probleme, wie Sie gleich noch sehen werden.
Die folgende Prozedur umfasst mehrere Schritte, die hier zunächst zusammengefasst und anschließend in Einzelschritten dargestellt werden:

1. Die Nachricht aba, cad, aca wandeln Sie - wie beschrieben - in Zahlen um.
2. Diese Darstellung, beispielhaft zur Basis 2²=4 (statt 2⁸=256), wandeln Sie in eine Darstellung zur Basis 10 um, damit Sie zur Verschlüsselung die Tabelle 1 benutzen können, in der die Zahlen ja auch auf 10er-Basis dargestellt werden. Dabei entsteht eine kodierte Nachricht zur Basis 10.
3. Um die Kodierung im Vergleich zum „Klartext“ zu erkennen, rechnen Sie die zur Basis 10 kodierte Nachricht auf die Basis 4 zurück und wandeln sie dann wieder in eine Buchstabensequenz.
4. So entsteht aus der Nachricht aba, cad, aca die verschlüsselte Nachricht dbb, ddd, dac.

Und nun ausführlich:

1. Die Nachricht aba, cad, aca wandeln Sie in Zahlen um.

   Angenommen, Sie beschränken sich bei den Nachrichten auf die 4 Buchstaben a, b, c und d. In diesem - wirklich sehr einfachen - Beispiel können Sie die vier Buchstaben durch die Zahlenwerte 0, 1, 2 und 3 darstellen und haben dann:

   a = 0, b = 1, c = 2  und  d = 3

   Verschlüsseln Sie nun die Nachricht aba, cad, aca. Sie kodieren diese Nachricht mit Hilfe der Primzahlen 7 und 11, mit dem öffentlichen Schlüssel 77 und 13 und dem dazugehörenden geheimen Schlüssel 37. Dieses Beispiel kennen Sie bereits aus dem früheren Kapitel: Sie haben damit die Tabellen 1 und 2 konstruiert.
   

2. Diese Darstellung zur Basis 4 wandeln Sie in eine Darstellung zur Basis 10 um. Damit können Sie zur Verschlüsselung die Tabelle 1 benutzen, in denen die Zahlen ja auch auf 10er-Basis dargestellt werden.

   Weil Sie vier Buchstaben für die Nachricht verwenden, rechnen Sie zur Basis 4. Für die Rechnung modulo 77 müssen Sie die Nachricht in Stücke von je drei Zeichen Länge zerlegen, weil die größte dreiziffrige Zahl zur Basis 4 die 333₄ ist. Zur Basis 10 hat diese Zahl den Wert 63.

   Würden Sie stattdessen die Nachricht in vier Zeichen lange Stücke zerlegen, würde 3333₄ den Wert 76₁₀ übersteigen und es würden unerwünschte Doppeldeutigkeiten entstehen.

   Folglich würde die Nachricht in dreiziffrigen Stücken nun

   aba, cad, aca

   ergeben. Geben Sie den Zeichen nun ihre Zahlenwerte und vergessen dabei nicht, dass die Stücke dreiziffrige Zahlen zur Basis 4 darstellen.

   Da Sie die Buchstaben durch die Zahlen a = 0, b = 1, c = 2, d = 3 darstellen, wird die Nachricht zu:

   010₄, 203₄, 020₄

   Zur Basis 10 wird diese Nachricht durch die Zahlenfolge 4, 35, 8 dargestellt. Warum? Nehmen Sie z.B. das mittlere Stück 203₄:

   3 * 4^0,	also  3 * 1,	also  3.
   0 * 4^1,	also  0 * 4,	also  0.
   2 * 4^2,	also  2 * 16,	also  32.

3. Jetzt können Sie zur Verschlüsselung die Tabelle 1 von Seite X benutzen, die ja zur Basis 10 berechnet wurde. Diese Tabelle benutzen wir, weil Sie mit dem schon bekannten Schlüsselpaar arbeiten wollen. Dabei entsteht eine kodierte Nachricht zur Basis 10.

   Zum Verschlüsseln der Nachricht nehmen Sie jetzt die o.g. Tabelle 1 zur Hilfe. Die Nachricht wird nun zu der Zahlenfolge 53, 63, 50 (zur Basis 10).
   

4. Wird sie nun wieder zur Basis 4 konvertiert, ergibt die Nachricht nun 311₄, 333₄, 302₄. Konvertiert man diese zu einer Buchstabensequenz, erhält man dbb, ddd, dac, was sich nun erheblich von der ursprünglichen Nachricht unterscheidet.

   Man kehrt nun also den Prozess um und transformiert die Zahlenfolge 53, 63, 50 mit Tabelle 2 und erhält die Sequenz 4, 35, 8. Und das entspricht als Zahlenfolge genau der ursprünglichen Nachricht.

   Anhand der Tabellen 1 und 2 können Sie ebenso gut Nachrichten unter Verwendung des geheimen Schlüssels (d.h., erst Tabelle 2 benutzen) verschlüsseln, dann mit dem öffentlichen Schlüssel (d.h., Tabelle 1 als zweites benutzen) dekodieren und damit Ihre ursprüngliche Zahl wieder herstellen. Das bedeutet, dass der Inhaber des geheimen Schlüssels damit Nachrichten unter Verwendung des RSA-Algorithmus verschlüsseln kann, die daher eindeutig nur von ihm stammen können.

Fazit:

Wie Sie gesehen haben, ist die ganze Angelegenheit zwar im Detail kompliziert, im Prinzip aber durchaus nachvollziehbar. Sie sollen schließlich nicht einer Methode einfach nur vertrauen, sondern ­- zumindest ansatzweise ­- ihre Funktionsweise durchschauen. Sehr viele tiefergehende Details sind leicht in anderen Büchern (z.B.: R. Wobst, „Abenteuer Kryptologie“) oder im Internet zu finden.

Immerhin wissen Sie nun: Wenn jemand sich an Ihren verschlüsselten E-Mails zu schaffen macht, ist er durchaus so lange damit beschäftigt, dass er nicht mehr erleben dürfte, diese dann noch lesen zu können...

25 GnuPG und das Geheimnis der großen Zahlen

Inhalt